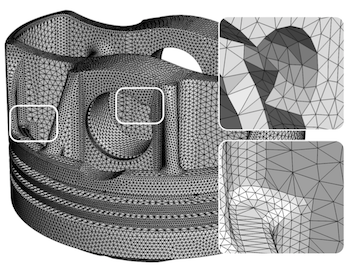
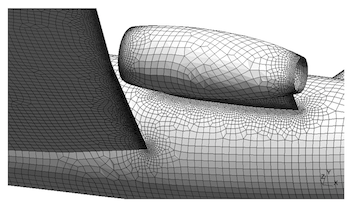
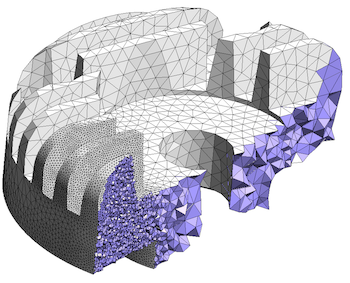
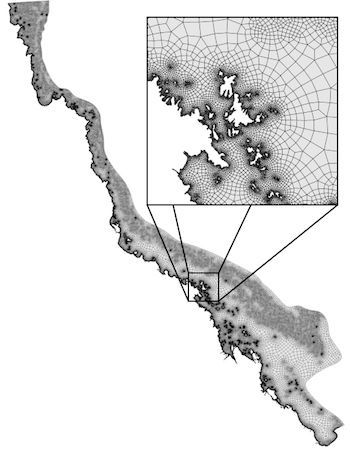

The goal of the Tetrahedron workshop is to gather both theoretical (computer science & applied mathematics) and practical (engineering & industry) specialists in the field of mesh generation, in view of numerical computations.
This fifth edition is organized at the University of Liège in Belgium by Christophe Geuzaine and Jean-François Remacle. The previous editions were hosted by the Weierstrass Institute in Berlin in 2005, by INRIA Rocquencourt in Paris in 2007, by the Swansea University in 2010, and by Politecnico di Milano in 2013.
Presentations are by invitation only; attendance is free thanks to our generous sponsors.
| July 4 | July 5 |
|---|---|
|
|
My personal journey to the fascinating world of geometric forms started 30 years ago with the invention of alpha shapes in the plane. It took about 10 years before we generalized the concept to higher dimensions, we produced working software with a graphics interface for the 3-dimensional case, and we added homology to the computations. Needless to say that this foreshadowed the inception of persistent homology, because it suggested the study of filtrations to capture the scale of a shape or data set. Importantly, this method has fast algorithms. The arguably most useful result on persistent homology is the stability of its diagrams under perturbations.
There is an increasing demand on generating many kinds of meshes in order to fit a particular purpose or numerical scheme. A non-exhaustive list includes the generation of adapted unstructured for mesh adaptation, quasi-structured or hybrid meshes, curvilinear, cartesian meshes... If the generation of each discretization has been mainly studied on its own, being able to generate all these kinds of meshes with a unique meshing technology remains a challenge. The scope of this talk is to illustrate the design of a unique cavity-based operator and show how many local mesh modification operators are recast in this framework. Numerical examples will include the generation of anisotropic, cartesian, hybrid and high-order meshes. We will also discuss its parallel extension.
Numerical PDE solvers heavily depend on mesh generation for accuracy, stability, and efficiency. Traditionally, element shape quality has been emphasized for finite elements and mesh generation. However, mesh resolution and overall mesh hierarchy have more fundamental and significant implications to modern numerical methods. We present an overview of some recent developments in numerical analysis to underline the advantages of hierarchical meshes and their associated challenges. We then describe some of our recent development on hierarchical unstructured meshes, including hierarchical mesh data structures, efficient generation and adaptation in serial and in parallel, and robust and high-order accurate treatment of surfaces. We also present some numerical examples and discuss about remaining challenges and future opportunities.
We present here an approach to generate automatically in parallel (whether multi-threaded or distributed) unstructured boundary layer tetrahedral meshes conforming to an input surface. Our approach segments the input data and builds internal interfaces defining volumes which can then be meshed in parallel on shared or distributed memory systems. The meshing process is driven by a continuous anisotropic sizing function, the volume vertices being inserted using a specific hybrid frontal-Delaunay algorithm. In order to generate boundary layer meshes, the classical front advancing algorithm is modified so as to insert, for each face of the front, vertices created by advancing along the face normal. Internal edges and faces are swapped when necessary to allow a combination of tetrahedra into prisms. Parallel results are shown on a few test cases.
The generation of isotropic unstructured grids with tetrahedral elements is by now a very mature area. The talk will therefore cover areas where improvements have been achieved in recent years. These are:
Complex geometric models often contain very small geometric features (e.g. holes and fillets) making necessary to produce extremely refined meshes in some regions of the domain. In general, it is necessary to invest a non-negligible amount of time removing these small features present in the CAD model before attempting to produce a mesh suitable for finite element analysis. The problem becomes particularly dramatic when different simulations are required in the same geometry. For instance, a geometric feature that is not relevant in a fluid mechanics problem could be extremely relevant when an acoustic problem is solved. Furthermore, features not relevant in electromagnetic simulations at low frequency can become extremely influential at higher frequencies.
In this talk, the first mesh generation technique that allows to produce meshes that account for the exact boundary representation of the domain irrespectively of the desired element size and the geometrical complexity will be presented.
Fully automatic methods for hexahedral meshing of solids with good quality elements have been under investigation for many years. The core problem is to determine the placement of mesh singularities, where other than 4 elements are connected to a given element edge. These singularities can run through the object between faces, or they can meet in the interior in a limited number of ways. There are several approaches which promise fully automatic hex mesh generation, but none has so far resulted in a robust solution for geometries of commercial complexity. Therefore it seems worthwhile to identify regions where certain known meshing techniques can be applied. This has the dual benefit of
The most useful and widely applied semi-automatic meshing technique is sweep meshing, where the pattern of quad mesh singularities is swept from source to target faces. In many aerospace components a substantial fraction of the part is composed of thin sheets. These thin sheet features can be identified by several techniques, after which a quad mesh on one of the bounding surfaces of the thin sheet can be swept through the thickness to create a hex mesh, i.e. the mesh singularities run from the ‘top’ bounding surface of the thin sheet through the thickness and out the ‘bottom’ surface. Similarly any long, slender features (like flanges or junctions in thin-walled structures) can be hex meshed by quad meshing a cross-section and sweeping the resulting pattern along the long slender region. The singularities run from the cross-section defining the source face to a target face which is also a cross-sectional face. For the remaining complex regions a simple analysis based on the corner angles and the Euler characteristic of each face can determine the net number of singularities that are required on that face. This provides a starting point for determining the necessary patterns of volume mesh singularities to create a hex mesh. For example, revolved features or sweeps with the same source and target faces features have no singularities on the external faces. Other meshing techniques like midpoint subdivision or multi-sweep techniques have recognisable singularity patterns. The use of virtual topology techniques to simplify the identification of singularity patterns will also be touched on.
In this talk, a method will be presented for goal-oriented space-time mesh adaptation. An output error-metric model is optimized to produce meshes which minimize error at fixed degrees of freedom. The output error-metric model incorporates fully-anisotropic error-metric dependence through synthesis of local solutions on embedded meshes. Applications of the method will be discussed for wave-dominated compressible flows, bluff body shedding, and porous media flows.
The application of high–order methods in industry requires meshing algorithms that generates valid and high-quality curved meshes. In this talk we present our framework to generate this kind meshes using an ‘a posteriori’ approach. The keystone of our approach is the definition of a quality measure for high-order meshes. One the one hand, this definition allows checking the validity and quality of a high-order mesh. On the other hand, it allows the generation of high-order curved meshes composed of valid and high-quality elements by optimizing a regularized version of the proposed mesh quality. Finally, we will present several examples to illustrate the main features and capabilities of the proposed framework.
The goal of our lecture is to explain the way we connect unstructured grid generation with CFD at Dassault-Aviation. For that purpose, several methods will be presented: advancing front method, adaptative grid generation, Delaunay method or topological manipulations (e.g. inlay grid or moving mesh). Finally, we will exemplify the different meshing techniques with industrial configurations.
One task in the numerical solution of partial differential equations is to define the computational mesh and its partition among the processors, for any given domain geometry. For many applications, it is desirable to perform all algorithms for adaptive mesh refinement (AMR) in parallel, in core, and whenever the simulation requires it. This imposes the conditions that AMR shall scale at least as well as the numerical solvers and that absolute runtimes of AMR algorithms shall be small.
Forest-of-octrees AMR is an approach that offers both geometric flexibility and parallel scalability. In this talk, we discuss the main conceptional ideas and technical implications. To provide a functional and well-proven example, we present central data structures and algorithmic concepts from our research into the p4est and t8code libraries. p4est is an implementation of adaptive hexahedra that is being used in several modern finite element codes. t8code is an effort that aims to unify hexahedral and tetrahedral tree-based AMR, introducing a new simplicial space filling curve. We close with recent numerical results.
Unstructured mesh generation for a large scale complex configuration currently requires significant computer resources in serial mode. Consequently, parallel implementations have been pursued by several developers to reduce the turnaround time. Scalability becomes a significant issue as the basic mesh generation process starts with an empty space and no structure to decompose. Without sub-domains a parallel implementation requires significant communication and introduction of sub-domains can impose internal boundaries that lead to potentially adverse artifacts in the final mesh. In the context of modern HPC computers with 100’s to 1000’s of processors, parallel implementation of unstructured mesh generation requires a multi-tiered approach for effective utilization of the resources available. We are considering the combination of large-scale parallelism through a domain decomposition like approach and fine-scale parallelism through algorithmic modification within each sub-domain. Initial development work will be presented for a new virtual boundary method of simple decomposition. Each virtual boundary is simply a limit for mesh generation within each sub-domain. The resulting exposed faces are then used as a true internal boundary interface for the adjacent sub-domain. Multiple passes with differing sub-domains available for each pass are utilized to insure final mesh continuity. Current work shows promise of scalability into the 100’s of processors without artifacts in the final mesh. Further scalability will require that each sub-domain utilize concurrent processing deep within the algorithms involved.
Restricted Voronoi diagrams are an essential building block for several applications, such as surface reconstruction, mesh generation or optimal transport. During this presentation, I will present ongoing work on the development of new algorithms for the computation of such diagrams in higher dimensions, based on nearest neighbor queries. Such an approach avoids the computation of the full Voronoi diagram, which becomes prohibitive in higher dimensions and can be unnecessary whenever the restriction domain only sparsely intersects the diagram.
The topic of this talk is mainly motivated by the boundary recovery problem in tetrahedral mesh generation, in which a given set of constraints, edges and faces, is required to be represented by the generated tetrahedral mesh. A theoretical difficulty in this problem is the existence of 3d (non-convex) indecomposable polyhedra, whose interior cannot be decomposed into a set of tetrahedra with its own vertices, such as the well-known Schönhardt polyhedron. Although it is known that any indecomposable polyhedra can be tetrahedralised by inserting a certain number of additional points, so-called Steiner points, it remains a challenging problem, when the Steiner points can only be placed in the interior. In this talk, we present new classes of indecomposable polyhedra obtained by generalizing some well-known examples, namely the Schönhardt and Bagemihl polyhedra, and the Chazelle polyhedron. Optimal number of Steiner points and efficient algorithm are presented to tetrahedralize these polyhedra.
There is no registration fee for the Tetrahedron workshop, but registration is mandatory. Registrations are now closed.
The organizers and the sponsors will support all lunches. Travel expenses, lodging and dinners are at the participants' own charge.
The workshop will be held at the University of Liège in Belgium, in the Opera complex in the city center:
Université de Liège, Opera complexTo reach the conference room, enter the building under the Galerie Opera sign and go to the +1 floor:
Free WiFi is available in the conference room through eduroam.
Nearby hotels include:
$)
$$)
$$$)
$$$)
The social activity and the banquet will take place at the Brasserie {C} (Impasse des Ursulines, B-4000 Liège).








